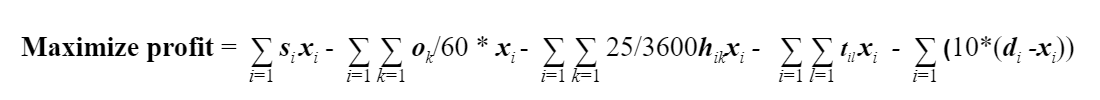Sophia Li.

Learn More

The WARP Shoe Company.

 

Determining an optimal production plan using AMPL and Gurobi optimization  

Github

Access Database

The WARP Shoe Company Project

  • Category: Programming, Optimization
  • Client: The University of Toronto
  • Project date: April 2021

Problem Statement 

At the beginning of year 2006, one of the major market competitors of WARP went bankrupt. Thus, WARP market analysts predict that for the month of February the demand for all types of shoes will double. Assume that closing inventory of January 2006 was zero for alltypes of shoes. Assume also that all sales happen at the end of the month. The management of WARP wants to know what is the most profitable production plan. This project is aimed at determining the optimal production strategy to achieve maximum profit for the WARP Shoe Company. 

Powering Crucial Business Decisions through Optimization

The WARP Shoe Project uses The Gurobi Optimizer and AMPL to mathematically determine an optimal production strategy for the fictional WARP Shoe company. The project uses a Microsoft Database file to retrieve information such as Product Price, Demand, and Production costs. After formulating a linear program to model the problem, .dat, .mod and .run files were generated in order to output the solution to an .out file.      

 

Technologies 

 Gurobi

 AMPL

 

Deliverables

.dat file: problem information

 .mod file: problem structure

 .run file: ampl commands

 .out file: Final objective function and optimal x-values 

Part I 

Problem Formulation

In addition to the information from the Access files, the following additional considerations/constraints were taken into account:

 

  •  The budget for raw materials is $10,000,000
  •  It has been decided that during February 2006 the WARP shoe production plant, including all machines, will work up to 12 hours a day, 28 days a month. The cost of operation of each machine is given in the Machine_Mastertable. Assume that setup times and costs are negligible. The amount of time (s) each shoe requires from each machine is given in the Machine_Assign table
  •  Workers are paid on an hourly basis at the rate of $25/hour. Each machine has to be operated by one worker

    •  

    Decision Variables

     

     Let xi be the number of shoes of type i to produce (i = 1, 2, 3, … , 557)

    Objective Function Variables

     

    • Let s(i) be the sale price of the shoes of type i ((i = 1, 2, 3, … , 557)
    • Let t(il) be the number of raw material used for raw material number l used for shoe type i (i = 1, 2, 3, … , 557) (l = 1, 2, 3, … , 165)
    • Let o(k) be the operations cost per minute of the machine number k (k = 1, 2, 3, … , 72)
    •  Let h(ik) be the average operation duration of the machine number k assigned to shoe type i (i = 1, 2, 3, … , 557) (k = 1, 2, 3, … , 72)
    •  Let d(i) be the demand of the shoes of type i (i = 1, 2, 3, … , 557)
    •  Let c(l) be the cost for the raw material number l (l = 1, 2, 3, … , 165)
    •  Let q(l) be the max amount of raw material available for the raw material number l (l = 1, 2, 3, … , 165)

The Objective Function

The decision variables, objective function, and constraints were modelled in AMPL to determine a optimal solution.

Part II 

Obtained Results

 

The project files (.dat, .mod, .run, .out) displayed in AMPL IDE

 

When solved using Gurobi, the optimal profit value was determined to be $18,555,382.32. The optimal x-values, which are the quantities of each type of shoe to produce, are determined to be the following: 

Passionate About Innovation

From multi-stage ideation to wire-frame prototyping, I am passionate about the intersection between technology and innovation and finding optimal solutions to modern day problems.

View My Work